Yield Strength Formula

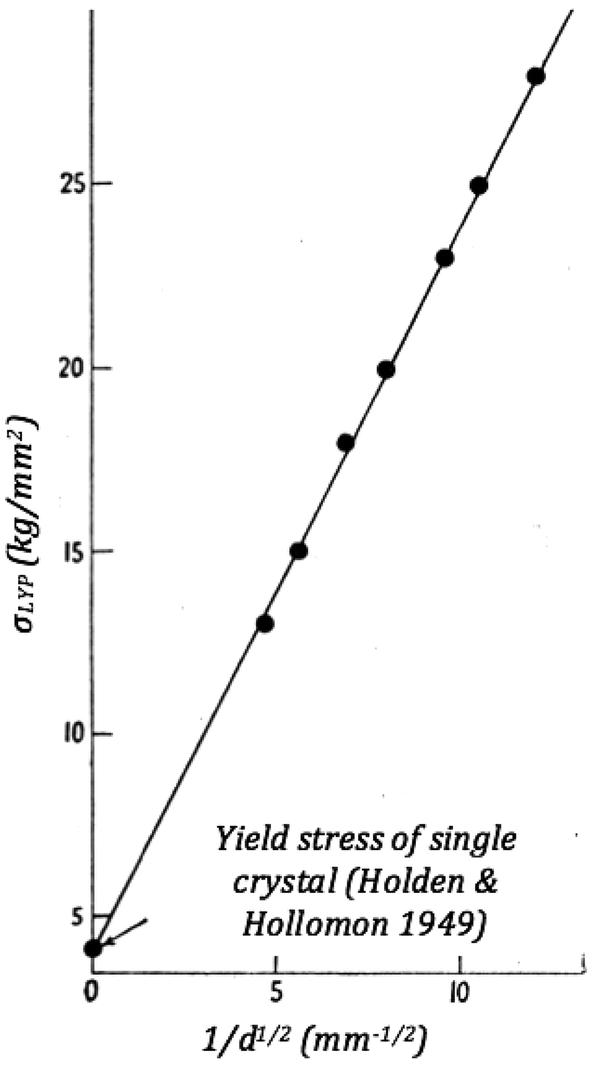
The yield strength or yield stress is a material property and is the stress corresponding to the yield point at which the material begins to deform plastically. The yield strength is often used to determine the maximum allowable load in a mechanical component, since it represents the upper limit to forces that can be applied without producing.

• Yield Strength Formula Beam
• Yield Strength Equation Modulus Of Elasticity
• Material Yield Strength

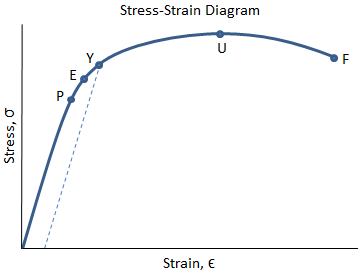
The yield strength, corresponding to the yield point, is often defined by an offset method.Line AB is drawn at a slope equal to Young's modulus.Point A corresponds to a definite or stated amount of permanent set, usually 0.2 percent of the original gauge length, although 0.01, 0.1, and 0.5 are occasionally used. In the case of aluminum and of many other ductile materials, the onset of yield. Before the first yield point, the material will have an elastic behavior, which means that it will go back to its initial state if we release the applied strength. Beyond the elastic limit, the material will have a plastic behavior, and permanent deformation will occur.

The minimum yield strength is the key property of steel used in pipeline design. See Figure 11.10.This figure shows the relationship between stress and strain. The minimum yield strength is defined as the tensile stress required to produce a total elongation of 0.5%. Tensile Yield Strength Unit Conversion Calculator; Unit Conversion Calculator & Converter for Tensile/Yield & Charpy values. Use the following calculator to convert yield or tensile values in ksi, Mpa, N/mm² or psi. Type the value in the box next to Mpa (using the drop down to change the unit of measurement).

In engineering, shear strength is the strength of a material or component against the type of yield or structural failure when the material or component fails in shear. A shear load is a force that tends to produce a sliding failure on a material along a plane that is parallel to the direction of the force. When a paper is cut with scissors, the paper fails in shear.

In structural and mechanical engineering, the shear strength of a component is important for designing the dimensions and materials to be used for the manufacture or construction of the component (e.g. beams, plates, or bolts). In a reinforced concrete beam, the main purpose of reinforcing bar (rebar) stirrups is to increase the shear strength. Slots era casino.

Wrotslavsky.

Equations[edit]

For shear stressτ{displaystyle tau } applies

τ=σ1−σ32,{displaystyle tau ={frac {sigma _{1}-sigma _{3}}{2}},}

where

σ1{displaystyle sigma _{1}} is major principal stress and

σ3{displaystyle sigma _{3}} is minor principal stress.

In general: ductile materials (e.g. aluminum) fail in shear, whereas brittle materials (e.g. cast iron) fail in tension. See tensile strength.

To calculate:

Given total force at failure (F) and the force-resisting area (e.g. the cross-section of a bolt loaded in shear), ultimate shear strength (τ{displaystyle tau }) is:

Yield Strength Formula Beam

τ=FA=Fπrbolt2=4Fπdbolt2{displaystyle tau ={frac {F}{A}}={frac {F}{pi r_{bolt}^{2}}}={frac {4F}{pi d_{bolt}^{2}}}}

For average shear stress

τ(avg)=VA{displaystyle tau scriptstyle (avg)={frac {V}{A}}}

where

τ(avg){displaystyle tau scriptstyle (avg)} is the average shear stress,

V{displaystyle V} is the shear force applied to each section of the part, and

A{displaystyle A} is the area of the section.^[1]

Average shear stress can also be defined as the total force of V{displaystyle V} as

V=∫τdA{displaystyle V=int tau dA}

This is only the average stress, actual stress distribution is not uniform. In real world applications, this equation only gives an approximation and the maximum shear stress would be higher. Stress is not often equally distributed across a part so the shear strength would need to be higher to account for the estimate.^[2]

Comparison[edit]

Yield Strength Equation Modulus Of Elasticity

As a very rough guide relating tensile, yield, and shear strengths:^[3]

In engineering, shear strength is the strength of a material or component against the type of yield or structural failure when the material or component fails in shear. A shear load is a force that tends to produce a sliding failure on a material along a plane that is parallel to the direction of the force. When a paper is cut with scissors, the paper fails in shear.

In structural and mechanical engineering, the shear strength of a component is important for designing the dimensions and materials to be used for the manufacture or construction of the component (e.g. beams, plates, or bolts). In a reinforced concrete beam, the main purpose of reinforcing bar (rebar) stirrups is to increase the shear strength. Slots era casino.

Wrotslavsky.

Equations[edit]

For shear stressτ{displaystyle tau } applies

τ=σ1−σ32,{displaystyle tau ={frac {sigma _{1}-sigma _{3}}{2}},}

where

σ1{displaystyle sigma _{1}} is major principal stress and

σ3{displaystyle sigma _{3}} is minor principal stress.

In general: ductile materials (e.g. aluminum) fail in shear, whereas brittle materials (e.g. cast iron) fail in tension. See tensile strength.

To calculate:

Given total force at failure (F) and the force-resisting area (e.g. the cross-section of a bolt loaded in shear), ultimate shear strength (τ{displaystyle tau }) is:

Yield Strength Formula Beam

τ=FA=Fπrbolt2=4Fπdbolt2{displaystyle tau ={frac {F}{A}}={frac {F}{pi r_{bolt}^{2}}}={frac {4F}{pi d_{bolt}^{2}}}}

For average shear stress

τ(avg)=VA{displaystyle tau scriptstyle (avg)={frac {V}{A}}}

where

τ(avg){displaystyle tau scriptstyle (avg)} is the average shear stress,

V{displaystyle V} is the shear force applied to each section of the part, and

A{displaystyle A} is the area of the section.^[1]

Average shear stress can also be defined as the total force of V{displaystyle V} as

V=∫τdA{displaystyle V=int tau dA}

This is only the average stress, actual stress distribution is not uniform. In real world applications, this equation only gives an approximation and the maximum shear stress would be higher. Stress is not often equally distributed across a part so the shear strength would need to be higher to account for the estimate.^[2]

Comparison[edit]

Yield Strength Equation Modulus Of Elasticity

As a very rough guide relating tensile, yield, and shear strengths:^[3]

USS: Ultimate Shear Strength, UTS: Ultimate Tensile Strength, SYS: Shear Yield Stress, TYS: Tensile Yield Stress

There are no published standard values for shear strength like with tensile and yield strength. Instead, it is common for it to be estimated as 60% of the ultimate tensile strength. Shear strength can be measured by a torsion test where it is equal to their torsional strength.^[4][5]

When values measured from physical samples are desired, a number of testing standards are available, covering different material categories and testing conditions. In the US, ASTM standards for measuring shear strength include ASTM B831, D732, D4255, D5379, and D7078. Internationally, ISO testing standards for shear strength include ISO 3597, 12579, and 14130.^[7]

See also[edit]

References[edit]

1. ^Hibbeler, Russell. Mechanics of materials. ISBN1-292-17828-0. OCLC1014358513.
2. ^'Mechanics eBook: Shear and Bearing Stress'. www.ecourses.ou.edu. Retrieved 2020-02-14.
3. ^'Shear Strength of Metals'. www.roymech.co.uk.
4. ^'Shear Strength - Instron'. www.instron.us. Retrieved 2020-02-14.
5. ^Portl; Portl, bolt com; Bolt; Company, Manufacturing; St, Inc 3441 NW Guam; Portl; PT547-6758, OR 97210 USA Hours: Monday-Friday 6 AM to 5 PM. 'Calculating Yield & Tensile Strength'. Portland Bolt. Retrieved 2020-02-14.
6. ^Watson, DC (May 1982). Mechanical Properties of E293/1581 Fiberglass-Epoxy Composite and of Several Adhesive Systems(PDF) (Technical report). Wright-Patterson Air Force, Ohio: Air Force Wright Aeronautical Laboratories. p. 16. Retrieved 24 October 2013.
7. ^S. Grynko, 'Material Properties Explained' (2012), ISBN1-4700-7991-7, p. 38.

Material Yield Strength